Projects

Reduced order modeling for stratified flows

Full Order Modeling

Reduced Order Modeling

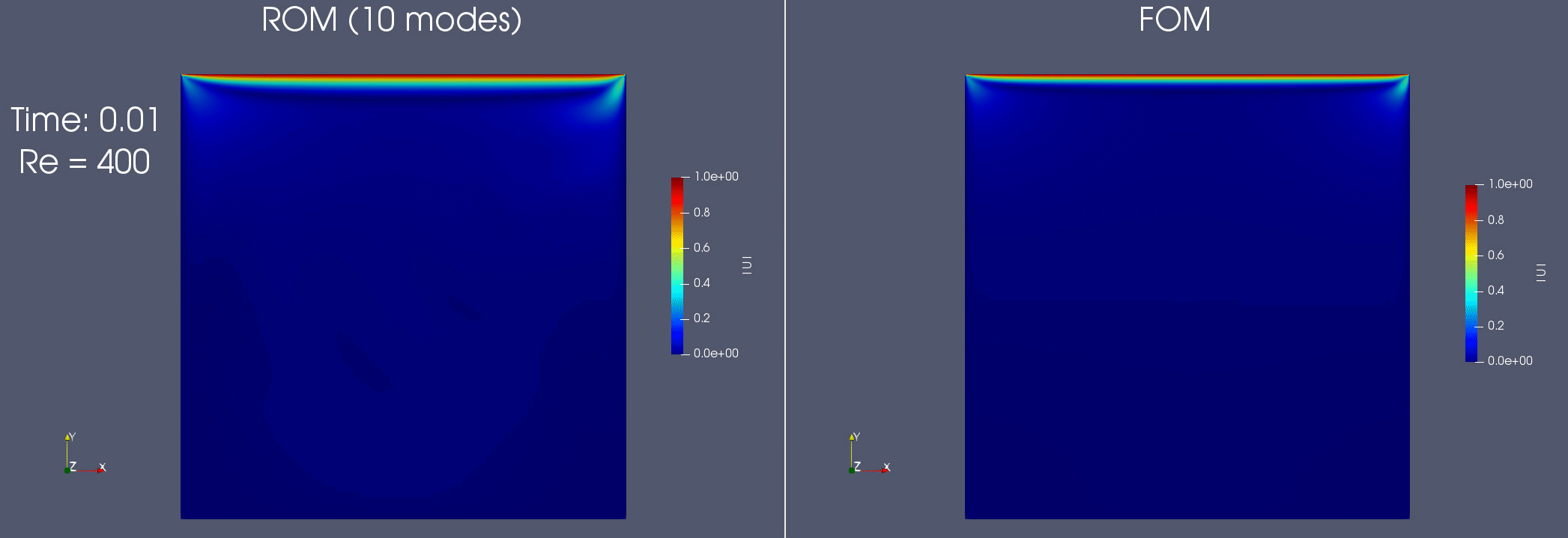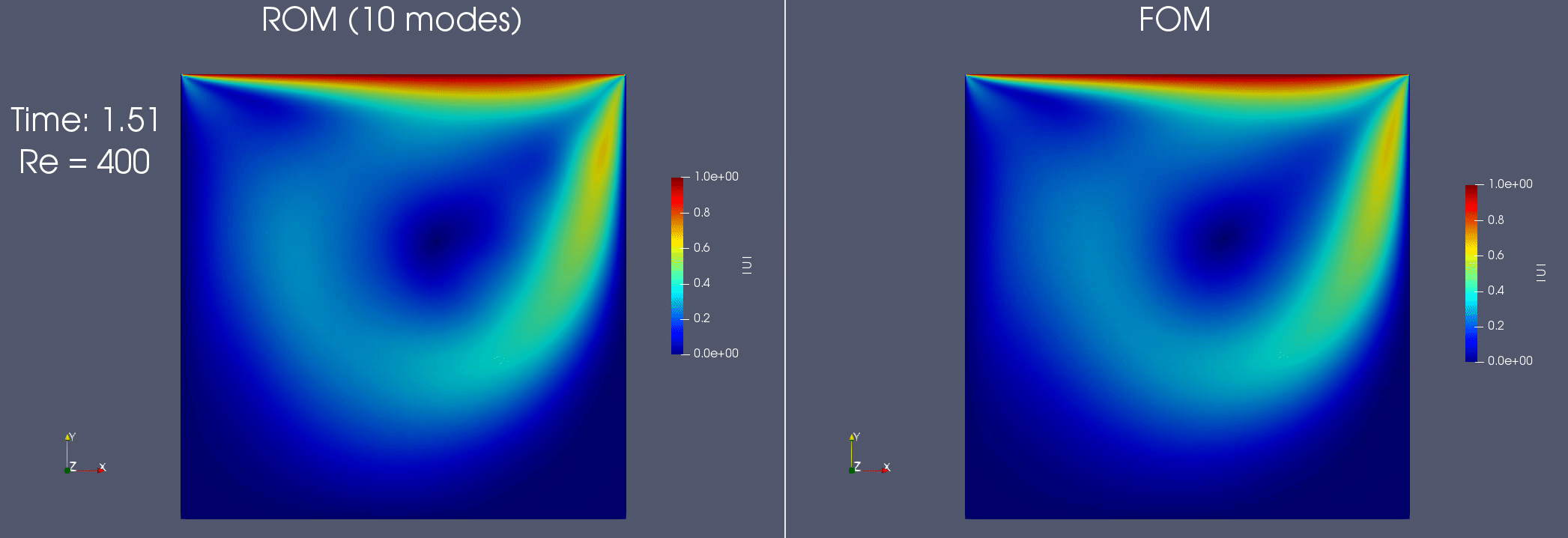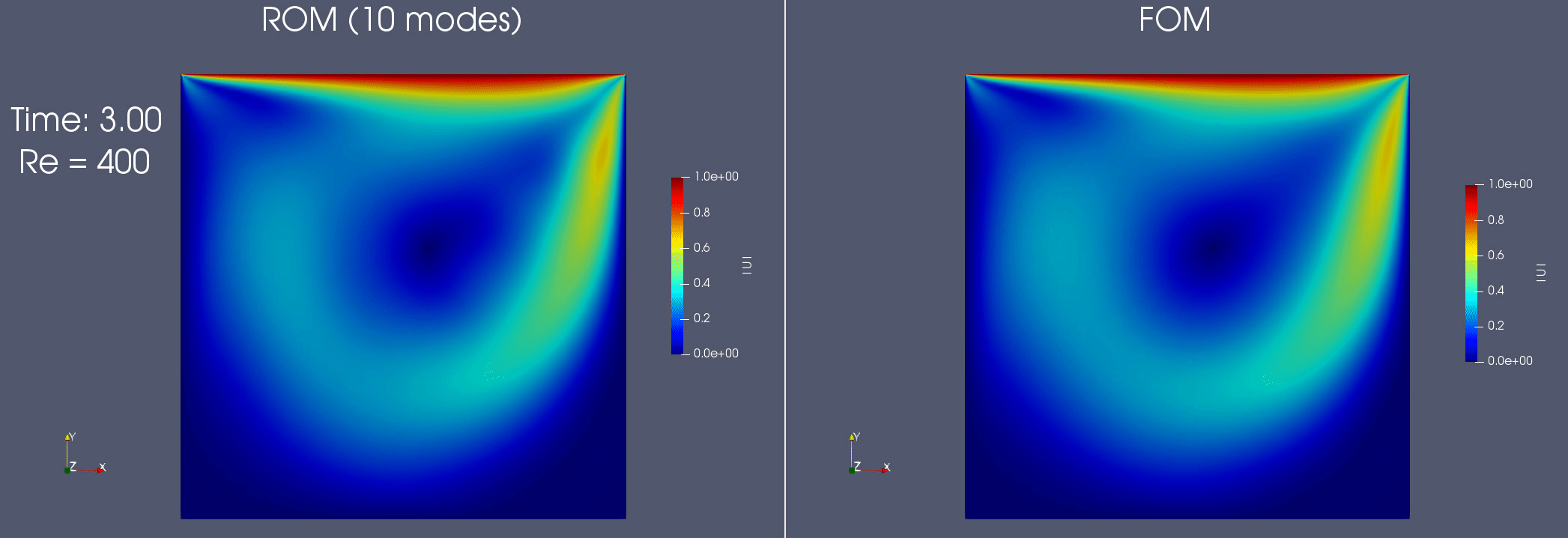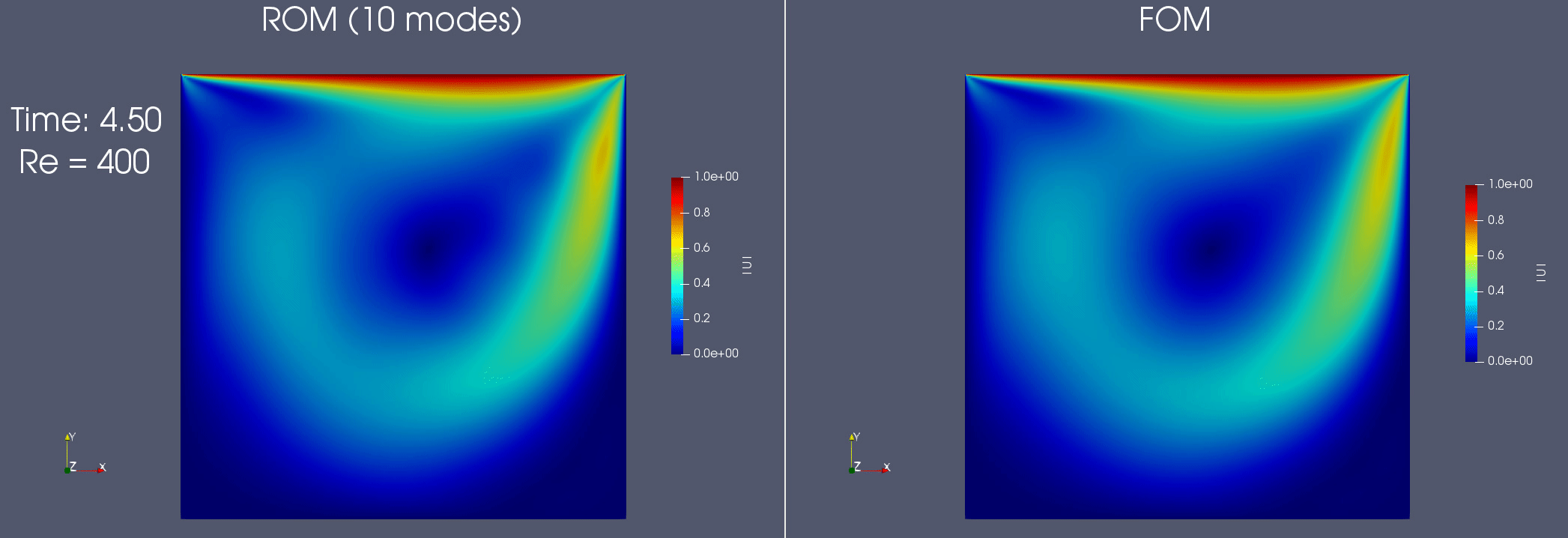
Reduced order modeling for incompressible flows

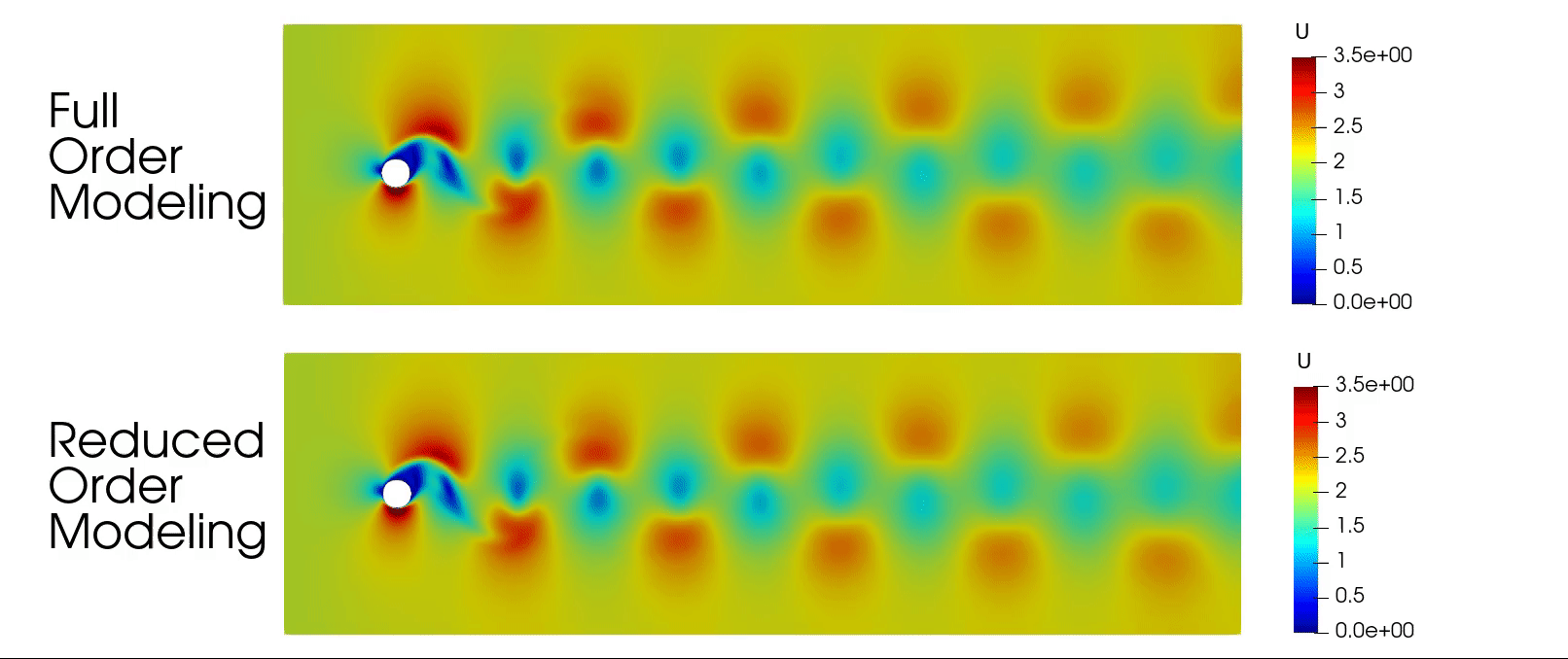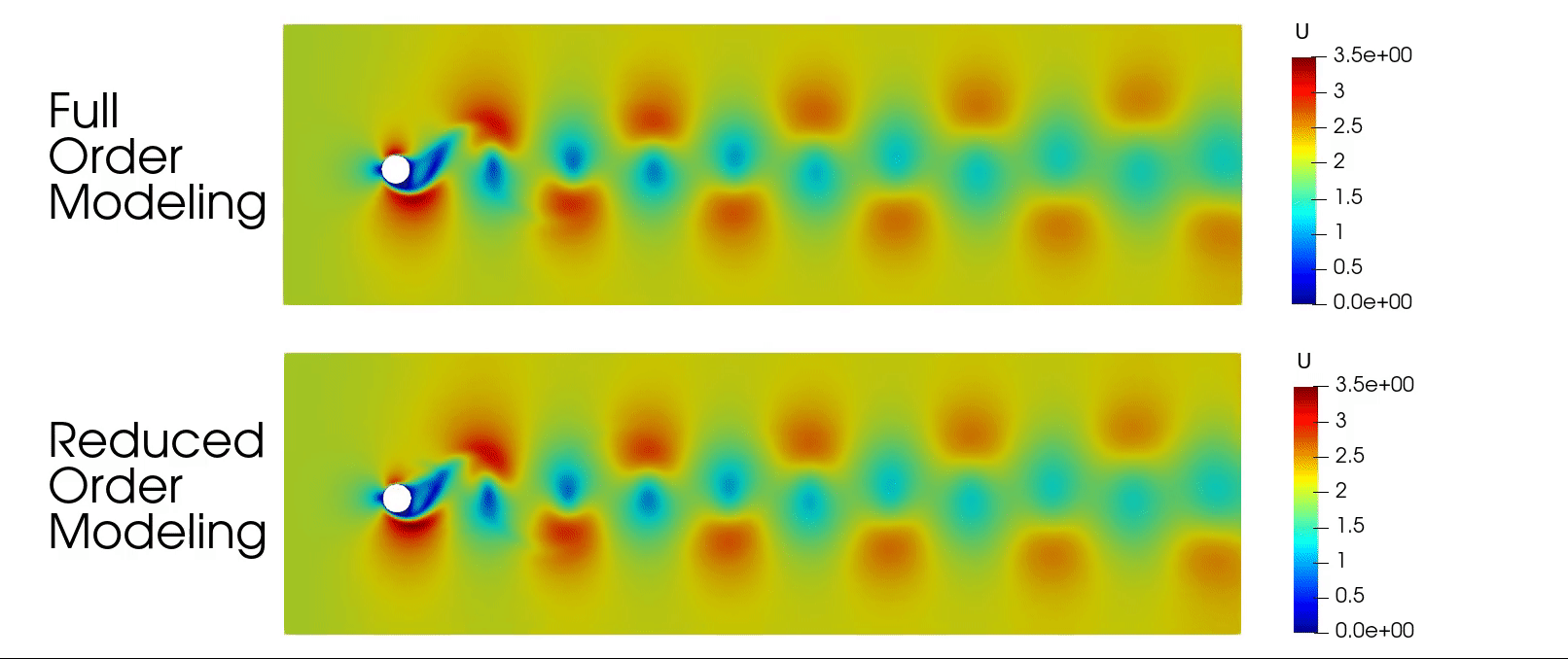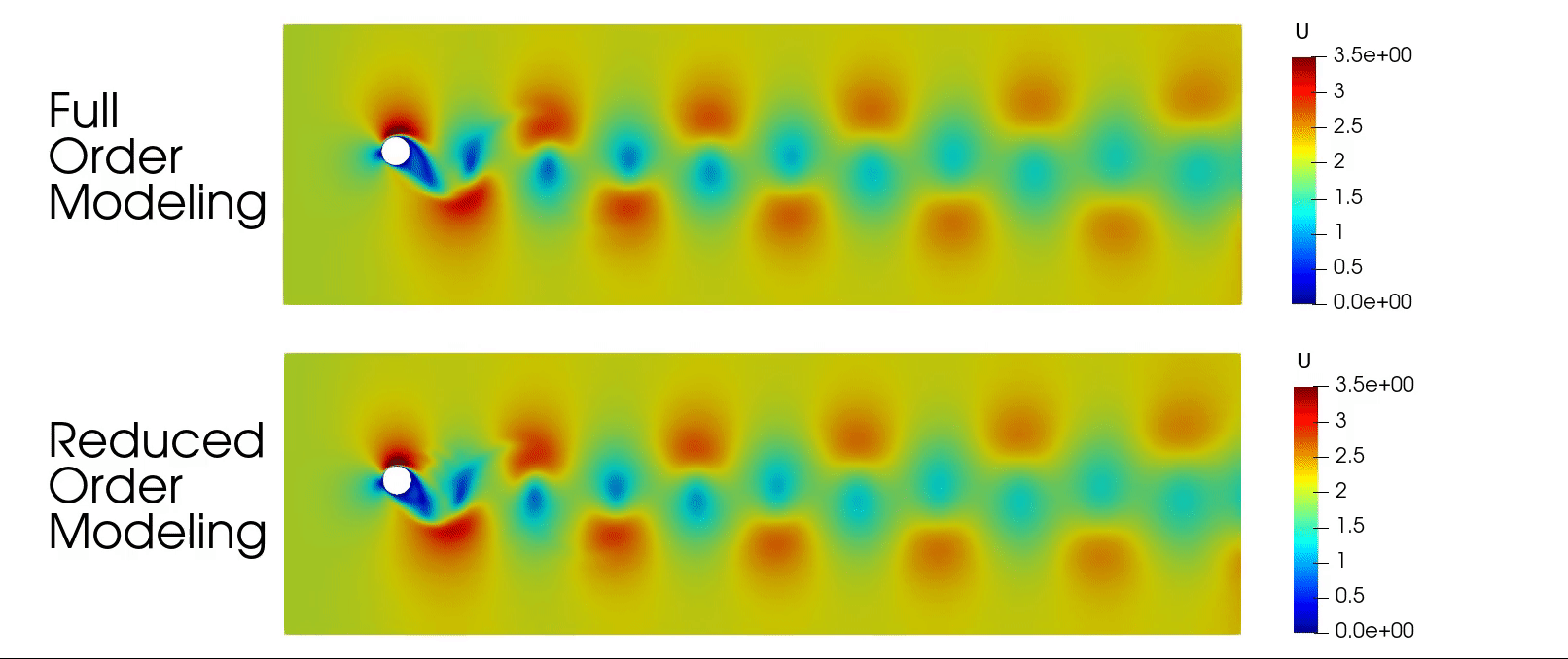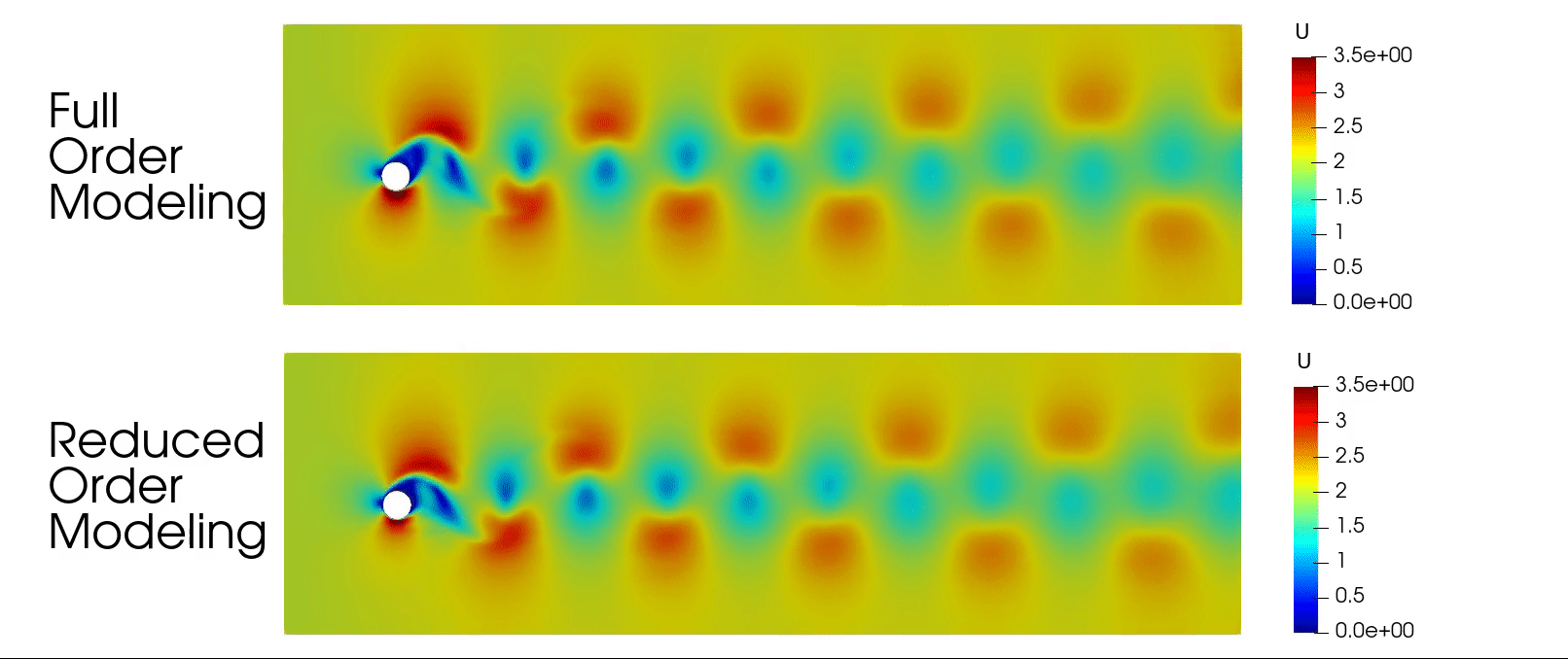
Discontinuous Galerkin for Compressible Euler Equations

Course: Computational Fluid Dynamics (MAE 766) Instructor: Dr. Hong Luo

📌 Problem: Solving the 2D Compressible Euler Equations for aerodynamic cases like flow around a NACA 0012 airfoil, a cylinder, and a channel with a bump using numerical methods. Traditional methods struggle with accuracy and efficiency for high-speed flows.

⚡ Challenges:

1. Handling hyperbolic partial differential equations accurately.

2. Implementing the Discontinuous Galerkin (DG) method while maintaining computational stability.

3. Resolving shock waves and flow separations in transonic and supersonic regimes.

🎯 Objectives Achieved:

1. Developed a DG-based finite volume solver using the Van-Leer flux vector splitting method.

2. Conducted a grid convergence study to validate results.

3. Successfully simulated subsonic, transonic, and supersonic flows, identifying shock locations and aerodynamic forces.

🔗 This project showcases my expertise in high-fidelity CFD methods and numerical discretization techniques. Find the full report here.

Finite Volume Method for Incompressible Navier-Stokes Equations

Course: Computational Fluid Mechanics and Heat Transfer (MAE 560) Instructor: Dr. Pramod Subbareddy

📌 Problem: Implementing a finite volume method (FVM) solver for the incompressible Navier-Stokes equations on a 2D quadrilateral mesh. The solver is validated using two benchmark problems:

1. Taylor-Green Vortex Decay – A test case for transient vortex dissipation.

2. Lid-Driven Cavity Flow – A classical problem in computational fluid dynamics (CFD).

⚡ Challenges:

1. Handling periodic boundary conditions for the Taylor-Green vortex problem.

2. Implementing the Mahesh Algorithm, a fractional step finite volume approach.

3. Ensuring numerical stability in the presence of high Reynolds number flows.

4. Achieving grid convergence and validating results with Ghia et al. (1982).

🎯 Objectives Achieved:

1. Developed a MATLAB-based FVM solver using structured quadrilateral grids.

2. Accurately simulated vortex dissipation and observed kinetic energy decay matching analytical solutions.

3. Modeled steady-state cavity flow, comparing results with spectral solutions from literature.

4. Identified limitations of explicit methods like Adams-Bashforth, highlighting trade-offs between computational cost and accuracy.

🔗 This project highlights my expertise in finite volume methods, incompressible flow solvers, and CFD benchmarking. Find the full report here.

Finite Element Program for Potential Flows

Course: Computational Fluid Dynamics (MAE 766) Instructor: Dr. Hong Luo

📌 Problem: Developing a 2D incompressible potential flow solver using the Finite Element Method (FEM) on unstructured grids. The solver is applied to two cases:

1. Internal flow in a channel with a bump

2. External flow around a cylinder

⚡ Challenges:

1. Implementing linear FEM for solving the Laplace equation governing potential flows.

2. Handling unstructured grids to model arbitrary flow domains.

3. Ensuring numerical convergence with mesh refinement.

🎯 Objectives Achieved:

1. Developed a FORTRAN-based FEM solver with Gauss-Seidel iteration for solving the Laplace equation.

2. Conducted a grid independence study, verifying that finer meshes led to lower numerical error.

3. Used Tecplot 360 for post-processing velocity potential, velocity magnitude, and vector fields.

🔗 This project demonstrates my expertise in finite element methods, numerical PDE solvers, and computational flow analysis. Find the full report here.

Discontinuous Galerkin for 1D Nonlinear Advection-Diffusion Equations

Course: Computational Fluid Dynamics (MAE 766) Instructor: Dr. Hong Luo

📌 Problem: Developing a 1D Discontinuous Galerkin (DG) solver for nonlinear advection-diffusion equations, which describe important physical transport phenomena such as heat transfer and wave propagation.

⚡ Challenges:

1. Implementing high-order numerical flux calculations for both diffusion (DDG formulation) and advection (upwinding method).

2. Handling nonlinear behavior in the advection-diffusion equation, which leads to shock wave formation.

3. Conducting convergence studies to verify numerical accuracy.

🎯 Objectives Achieved:

1. Implemented a DG(P1) solver using Taylor nodal basis functions to solve the Heat Equation and nonlinear advection-diffusion equation.

2. Used the Direct Discontinuous Galerkin (DDG) formulation to calculate diffusive fluxes efficiently.

3. Verified results by comparing numerical solutions with exact solutions and performing a convergence study.

4. Demonstrated how nonlinear effects cause a sine wave to evolve into a shock wave over time.

🔗 This project highlights my expertise in high-order numerical methods for PDEs, DG schemes, and nonlinear transport phenomena modeling. Find the full report here.

Not-A-Knot Cublic Spline Interpolation

Course: Computational Methods in Engineering (MAE 589) Instructor: Dr. Hong Luo

📌 Problem: Interpolating complex data points accurately using piecewise cubic polynomials. Traditional polynomial interpolation often results in Runge’s phenomenon, where oscillations occur for high-degree polynomials.

⚡ Challenges:

1. Ensuring smoothness and accuracy in the interpolation process.

2. Avoiding ill-conditioned matrices that arise in high-degree polynomial interpolation.

3. Applying Not-A-Knot boundary conditions for a globally smooth curve.

🎯 Objectives Achieved:

1. Implemented Not-A-Knot cubic spline interpolation in FORTRAN.

2. Validated accuracy by interpolating the Runge function and analyzing error trends.

3. Extended the method to parametric cubic splines, successfully interpolating a circle with 9 points.

🔗 This project highlights my skills in numerical methods, computational programming, and data approximation techniques. Find the full report here.